Apply running function — runner • runner

Applies custom function on running windows.

runner(
  x,
  f = function(x) x,
  k = integer(0),
  lag = integer(1),
  idx = integer(0),
  at = integer(0),
  na_pad = FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

# S3 method for default
runner(
  x,
  f = function(x) x,
  k = integer(0),
  lag = integer(1),
  idx = integer(0),
  at = integer(0),
  na_pad = FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

# S3 method for data.frame
runner(
  x,
  f = function(x) x,
  k = attr(x, "k"),
  lag = if (!is.null(attr(x, "lag"))) attr(x, "lag") else integer(1),
  idx = attr(x, "idx"),
  at = attr(x, "at"),
  na_pad = if (!is.null(attr(x, "na_pad"))) attr(x, "na_pad") else FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

# S3 method for grouped_df
runner(
  x,
  f = function(x) x,
  k = attr(x, "k"),
  lag = if (!is.null(attr(x, "lag"))) attr(x, "lag") else integer(1),
  idx = attr(x, "idx"),
  at = attr(x, "at"),
  na_pad = if (!is.null(attr(x, "na_pad"))) attr(x, "na_pad") else FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

# S3 method for matrix
runner(
  x,
  f = function(x) x,
  k = integer(0),
  lag = integer(1),
  idx = integer(0),
  at = integer(0),
  na_pad = FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

# S3 method for xts
runner(
  x,
  f = function(x) x,
  k = integer(0),
  lag = integer(1),
  idx = integer(0),
  at = integer(0),
  na_pad = FALSE,
  simplify = TRUE,
  cl = NULL,
  ...
)

Arguments

x: (vector, data.frame, matrix, xts, grouped_df)
Input in runner custom function f.
f: (function)
Applied on windows created from x. This function is meant to summarize windows and create single element for each window, but one can also specify function which return multiple elements (runner output will be a list). By default runner returns windows as is (f = function(x)).
k: (integer vector or single value)
Denoting size of the running window. If k is a single value then window size is constant for all elements, otherwise if length(k) == length(x) different window size for each element. One can also specify k in the same way as by argument in base::seq.POSIXt(). See 'Specifying time-intervals' in details section.
lag: (integer vector or single value)
Denoting window lag. If lag is a single value then window lag is constant for all elements, otherwise if length(lag) == length(x) different window size for each element. Negative value shifts window forward. One can also specify lag in the same way as by argument in base::seq.POSIXt(). See 'Specifying time-intervals' in details section.
idx: (integer, Date, POSIXt)
Optional integer vector containing sorted (ascending) index of observation. By default idx is index incremented by one. User can provide index with varying increment and with duplicated values. If specified then k and lag are depending on idx. Length of idx have to be equal of length x.
at: (integer, Date, POSIXt, character vector)
Vector of any size and any value defining output data points. Values of the vector defines the indexes which data is computed at. Can be also POSIXt sequence increment used in at argument in base::seq.POSIXt(). See 'Specifying time-intervals' in details section.
na_pad: (logical single value)
Whether incomplete window should return NA (if na_pad = TRUE) Incomplete window is when some parts of the window are out of range.
simplify: (logical or character value)
should the result be simplified to a vector, matrix or higher dimensional array if possible. The default value, simplify = TRUE, returns a vector or matrix if appropriate, whereas if simplify = "array" the result may be an array of "rank" (=length(dim(.))) one higher than the result of output from the function f for each window. Consequences of simplify in runner are identical to sapply.
cl: (cluster) experimental
Create and pass the cluster to the runner function to run each window calculation in parallel. See parallel::makeCluster() in details.
...: (optional)
other arguments passed to the function f.

Value

vector with aggregated values for each window. Length of output is the same as length(x) or length(at) if specified. Type of the output depends on the output from a function f.

Details

Function can apply any R function on running windows defined by x, k, lag, idx and at. Running window can be calculated on several ways:

Cumulative windows
applied when user doesn't specify k argument or specify k = length(x), this would mean that k is equal to number of available elements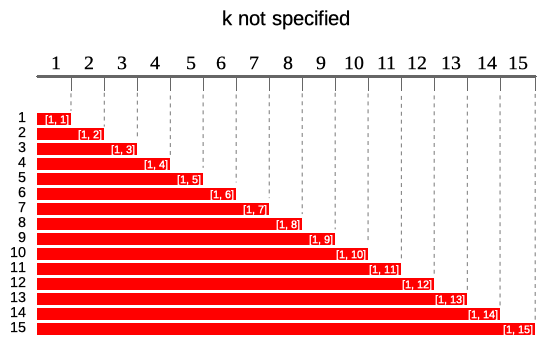
Constant sliding windows applied when user specify k as constant value keeping idx and at unspecified. lag argument shifts windows left (lag > 0) or right (lag < 0).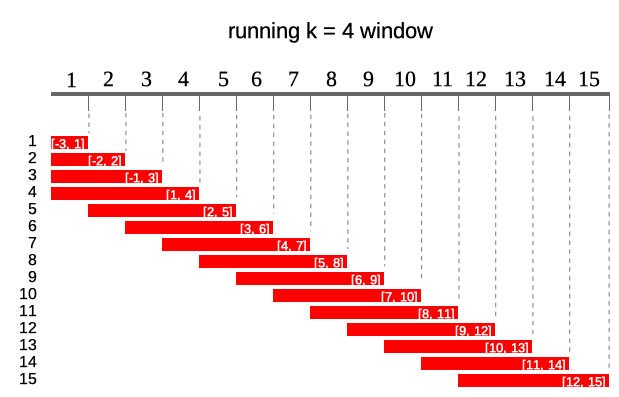
Windows depending on date
If one specifies idx this would mean that output windows size might change in size because of unequally spaced indexes. Fox example 5-period window is different than 5-element window, because 5-period window might contain any number of observation (7-day mean is not the same as 7-element mean)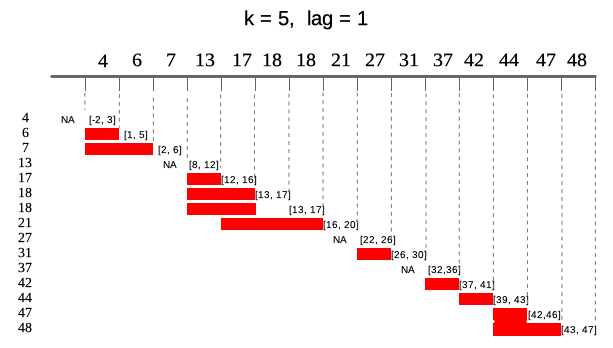
Window at specific indices
runner by default returns vector of the same size as x unless one specifies at argument. Each element of at is an index on which runner calculates function - which means that output of the runner is now of length equal to at. Note that one can change index of x by specifying idx. Illustration below shows output of runner for at = c(18, 27, 45, 31) which gives windows in ranges enclosed in square brackets. Range for at = 27 is [22, 26] which is not available in current indices.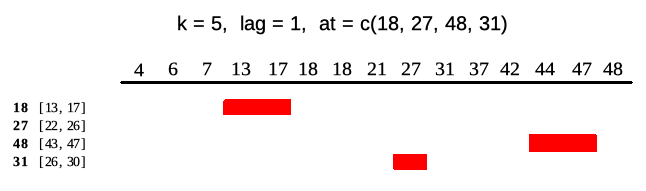

Specifying time-intervals

at can also be specified as interval of the output defined by at = "<increment>" which results in indices sequence defined by seq.POSIXt(min(idx), max(idx), by = "<increment>"). Increment of sequence is the same as in base::seq.POSIXt() function. It's worth noting that increment interval can't be more frequent than interval of idx - for Date the most frequent time-unit is a "day", for POSIXt a sec.

k and lag can also be specified as using time sequence increment. Available time units are "sec", "min", "hour", "day", "DSTday", "week", "month", "quarter" or "year". To increment by number of units one can also specify <number> <unit>s for example lag = "-2 days", k = "5 weeks".

Setting k and lag as a sequence increment can be also a vector can be a vector which allows to stretch and lag/lead each window freely on in time (on indices).

Parallel computing

Beware that executing R call in parallel not always have the edge over single-thread even if the cl <- registerCluster(detectCores()) was specified before.
Parallel windows are executed in the independent environment, which means that objects other than function arguments needs to be copied to the parallel environment using parallel::clusterExport(). For example using f = function(x) x + y + z will result in error as clusterExport(cl, varlist = c("y", "z")) needs to be called before.

Examples


# runner returns windows as is by default
runner(1:10)
#> [[1]]
#> [1] 1
#> 
#> [[2]]
#> [1] 1 2
#> 
#> [[3]]
#> [1] 1 2 3
#> 
#> [[4]]
#> [1] 1 2 3 4
#> 
#> [[5]]
#> [1] 1 2 3 4 5
#> 
#> [[6]]
#> [1] 1 2 3 4 5 6
#> 
#> [[7]]
#> [1] 1 2 3 4 5 6 7
#> 
#> [[8]]
#> [1] 1 2 3 4 5 6 7 8
#> 
#> [[9]]
#> [1] 1 2 3 4 5 6 7 8 9
#> 
#> [[10]]
#>  [1]  1  2  3  4  5  6  7  8  9 10
#> 

# mean on k = 3 elements windows
runner(1:10, f = mean, k = 3)
#>  [1] 1.0 1.5 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

# mean on k = 3 elements windows with different specification
runner(1:10, k = 3, f = function(x) mean(x, na.rm = TRUE))
#>  [1] 1.0 1.5 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

# concatenate two columns
runner(
  data.frame(
    a = letters[1:10],
    b = 1:10
  ),
  f = function(x) paste(paste0(x$a, x$b), collapse = "+")
)
#>  [1] "a1"                             "a1+b2"                         
#>  [3] "a1+b2+c3"                       "a1+b2+c3+d4"                   
#>  [5] "a1+b2+c3+d4+e5"                 "a1+b2+c3+d4+e5+f6"             
#>  [7] "a1+b2+c3+d4+e5+f6+g7"           "a1+b2+c3+d4+e5+f6+g7+h8"       
#>  [9] "a1+b2+c3+d4+e5+f6+g7+h8+i9"     "a1+b2+c3+d4+e5+f6+g7+h8+i9+j10"

# concatenate two columns with additional argument
runner(
  data.frame(
    a = letters[1:10],
    b = 1:10
  ),
  f = function(x, xxx) {
    paste(paste0(x$a, xxx, x$b), collapse = " + ")
  },
  xxx = "..."
)
#>  [1] "a...1"                                                                         
#>  [2] "a...1 + b...2"                                                                 
#>  [3] "a...1 + b...2 + c...3"                                                         
#>  [4] "a...1 + b...2 + c...3 + d...4"                                                 
#>  [5] "a...1 + b...2 + c...3 + d...4 + e...5"                                         
#>  [6] "a...1 + b...2 + c...3 + d...4 + e...5 + f...6"                                 
#>  [7] "a...1 + b...2 + c...3 + d...4 + e...5 + f...6 + g...7"                         
#>  [8] "a...1 + b...2 + c...3 + d...4 + e...5 + f...6 + g...7 + h...8"                 
#>  [9] "a...1 + b...2 + c...3 + d...4 + e...5 + f...6 + g...7 + h...8 + i...9"         
#> [10] "a...1 + b...2 + c...3 + d...4 + e...5 + f...6 + g...7 + h...8 + i...9 + j...10"

# number of unique values in each window (varying window size)
runner(letters[1:10],
  k = c(1, 2, 2, 4, 5, 5, 5, 5, 5, 5),
  f = function(x) length(unique(x))
)
#>  [1] 1 2 2 4 5 5 5 5 5 5

# concatenate only on selected windows index
runner(letters[1:10],
  f = function(x) paste(x, collapse = "-"),
  at = c(1, 5, 8)
)
#> [1] "a"               "a-b-c-d-e"       "a-b-c-d-e-f-g-h"

# 5 days mean
idx <- c(4, 6, 7, 13, 17, 18, 18, 21, 27, 31, 37, 42, 44, 47, 48)
runner::runner(
  x = idx,
  k = "5 days",
  lag = 1,
  idx = Sys.Date() + idx,
  f = function(x) mean(x)
)
#>  [1]       NA  4.00000  5.00000       NA 13.00000 15.00000 15.00000 17.66667
#>  [9]       NA 27.00000       NA 37.00000 42.00000 43.00000 45.50000

# 5 days mean at 4-indices
runner::runner(
  x = 1:15,
  k = 5,
  lag = 1,
  idx = idx,
  at = c(18, 27, 48, 31),
  f = mean
)
#> [1]  4.5   NA 13.5  9.0

# runner with data.frame
df <- data.frame(
  a = 1:13,
  b = 1:13 + rnorm(13, sd = 5),
  idx = seq(as.Date("2022-02-22"), as.Date("2023-02-22"), by = "1 month")
)
runner(
  x = df,
  idx = "idx",
  at = "6 months",
  f = function(x) {
    cor(x$a, x$b)
  }
)
#> [1]        NA 0.6571997 0.6924993

# parallel computing
library(parallel)
data <- data.frame(
  a = runif(100),
  b = runif(100),
  idx = cumsum(sample(rpois(100, 5)))
)
const <- 0
cl <- makeCluster(1)
clusterExport(cl, "const", envir = environment())

runner(
  x = data,
  k = 10,
  f = function(x) {
    cor(x$a, x$b) + const
  },
  idx = "idx",
  cl = cl
)
#>   [1]          NA  1.00000000  1.00000000  0.01724492 -0.09315799 -0.99327925
#>   [7] -0.94382033 -0.99710574 -0.98260307  0.65135545  0.87152732 -1.00000000
#>  [13] -1.00000000  1.00000000 -0.52128291 -0.05780382 -0.84347254 -1.00000000
#>  [19]  1.00000000 -0.76077380 -0.74453011  1.00000000          NA -1.00000000
#>  [25] -0.89962234 -0.89611962 -0.97093250 -1.00000000  1.00000000 -1.00000000
#>  [31]  1.00000000 -0.86400080          NA  1.00000000 -0.86775397  1.00000000
#>  [37] -1.00000000 -1.00000000 -1.00000000 -0.28843542 -0.67221825 -0.19909563
#>  [43]  0.11264234  1.00000000 -0.19349216  1.00000000  0.98477621  0.72549665
#>  [49]  1.00000000 -1.00000000 -1.00000000  0.48611613  0.13342545  0.16255224
#>  [55]  1.00000000  1.00000000  1.00000000 -0.37969457 -0.22479115 -1.00000000
#>  [61] -1.00000000 -0.29664241  1.00000000  0.52830307 -0.98104983 -0.97031468
#>  [67] -0.66148555  1.00000000  0.99504392  0.11134679  0.07975996 -0.74401064
#>  [73] -0.62841711 -1.00000000  1.00000000  0.34947453 -1.00000000 -0.77948953
#>  [79] -0.99239039 -0.80128888  1.00000000 -1.00000000          NA  1.00000000
#>  [85] -1.00000000  1.00000000 -1.00000000 -1.00000000  1.00000000 -0.42008586
#>  [91] -1.00000000 -1.00000000 -1.00000000  1.00000000  1.00000000 -0.35597197
#>  [97]  0.64812183  1.00000000  1.00000000  1.00000000
stopCluster(cl)

# runner with matrix
data <- matrix(data = runif(100, 0, 1), nrow = 20, ncol = 5)
runner(
  x = data,
  f = function(x) {
    tryCatch(
      cor(x),
      error = function(e) NA
    )
  }
)
#>       [,1] [,2]        [,3]        [,4]         [,5]        [,6]        [,7]
#>  [1,]   NA    1  1.00000000  1.00000000  1.000000000  1.00000000  1.00000000
#>  [2,]   NA    1  0.56501046  0.48501747  0.352903529  0.26309989  0.35214652
#>  [3,]   NA   -1  0.14209151 -0.30004551 -0.329346327 -0.29699283 -0.32498736
#>  [4,]   NA    1  0.78008109  0.64534982  0.542463283  0.46211608  0.49916964
#>  [5,]   NA   -1 -0.80337202 -0.70882472 -0.469876500 -0.42896778 -0.49174199
#>  [6,]   NA    1  0.56501046  0.48501747  0.352903529  0.26309989  0.35214652
#>  [7,]   NA    1  1.00000000  1.00000000  1.000000000  1.00000000  1.00000000
#>  [8,]   NA   -1  0.89699524  0.42711476  0.445763254  0.56340018  0.40437947
#>  [9,]   NA    1 -0.07548312 -0.05770721 -0.015884496  0.37926219  0.44647719
#> [10,]   NA   -1  0.03740517  0.02915300  0.250775474 -0.15275134 -0.38179867
#> [11,]   NA   -1  0.14209151 -0.30004551 -0.329346327 -0.29699283 -0.32498736
#> [12,]   NA   -1  0.89699524  0.42711476  0.445763254  0.56340018  0.40437947
#> [13,]   NA    1  1.00000000  1.00000000  1.000000000  1.00000000  1.00000000
#> [14,]   NA   -1 -0.50848709 -0.03041053 -0.006640857  0.20757600  0.15674132
#> [15,]   NA    1  0.47528311  0.10218339  0.163428041 -0.03575711  0.05739739
#> [16,]   NA    1  0.78008109  0.64534982  0.542463283  0.46211608  0.49916964
#> [17,]   NA    1 -0.07548312 -0.05770721 -0.015884496  0.37926219  0.44647719
#> [18,]   NA   -1 -0.50848709 -0.03041053 -0.006640857  0.20757600  0.15674132
#> [19,]   NA    1  1.00000000  1.00000000  1.000000000  1.00000000  1.00000000
#> [20,]   NA   -1 -0.99927272 -0.99527357 -0.034434260 -0.27056851 -0.36035489
#> [21,]   NA   -1 -0.80337202 -0.70882472 -0.469876500 -0.42896778 -0.49174199
#> [22,]   NA   -1  0.03740517  0.02915300  0.250775474 -0.15275134 -0.38179867
#> [23,]   NA    1  0.47528311  0.10218339  0.163428041 -0.03575711  0.05739739
#> [24,]   NA   -1 -0.99927272 -0.99527357 -0.034434260 -0.27056851 -0.36035489
#> [25,]   NA    1  1.00000000  1.00000000  1.000000000  1.00000000  1.00000000
#>             [,8]        [,9]         [,10]        [,11]       [,12]
#>  [1,]  1.0000000  1.00000000  1.000000e+00  1.000000000  1.00000000
#>  [2,]  0.3196817  0.17045850  9.150219e-05  0.139865415  0.23166354
#>  [3,] -0.1207477  0.20493548  2.625496e-01  0.369468178  0.44879964
#>  [4,]  0.5784996  0.68349574  5.426259e-01  0.574674672  0.61864992
#>  [5,] -0.3558083 -0.13510526 -1.685249e-02 -0.019104038 -0.14534561
#>  [6,]  0.3196817  0.17045850  9.150219e-05  0.139865415  0.23166354
#>  [7,]  1.0000000  1.00000000  1.000000e+00  1.000000000  1.00000000
#>  [8,]  0.3453758  0.22964343  1.828537e-01  0.329651436  0.42928727
#>  [9,]  0.3340412  0.23121032  2.278110e-01  0.296851354  0.38113586
#> [10,] -0.3768547 -0.39609429 -4.156059e-01 -0.382365655 -0.47256783
#> [11,] -0.1207477  0.20493548  2.625496e-01  0.369468178  0.44879964
#> [12,]  0.3453758  0.22964343  1.828537e-01  0.329651436  0.42928727
#> [13,]  1.0000000  1.00000000  1.000000e+00  1.000000000  1.00000000
#> [14,]  0.3845756  0.51971276  5.103827e-01  0.547196234  0.61128882
#> [15,]  0.1696688  0.26079361  2.796791e-01  0.247699648  0.02145079
#> [16,]  0.5784996  0.68349574  5.426259e-01  0.574674672  0.61864992
#> [17,]  0.3340412  0.23121032  2.278110e-01  0.296851354  0.38113586
#> [18,]  0.3845756  0.51971276  5.103827e-01  0.547196234  0.61128882
#> [19,]  1.0000000  1.00000000  1.000000e+00  1.000000000  1.00000000
#> [20,] -0.1142165  0.00944566  7.640232e-03  0.005231241 -0.14003288
#> [21,] -0.3558083 -0.13510526 -1.685249e-02 -0.019104038 -0.14534561
#> [22,] -0.3768547 -0.39609429 -4.156059e-01 -0.382365655 -0.47256783
#> [23,]  0.1696688  0.26079361  2.796791e-01  0.247699648  0.02145079
#> [24,] -0.1142165  0.00944566  7.640232e-03  0.005231241 -0.14003288
#> [25,]  1.0000000  1.00000000  1.000000e+00  1.000000000  1.00000000
#>              [,13]        [,14]        [,15]       [,16]       [,17]
#>  [1,]  1.000000000  1.000000000  1.000000000  1.00000000  1.00000000
#>  [2,]  0.125163001  0.123106833  0.115106112  0.11940811  0.03083497
#>  [3,]  0.480509687  0.452726283  0.449674348  0.41564975  0.18627580
#>  [4,]  0.408377521  0.393041092  0.331180263  0.31402514  0.25898383
#>  [5,] -0.180874381 -0.199955662 -0.191972166 -0.19437788 -0.13941943
#>  [6,]  0.125163001  0.123106833  0.115106112  0.11940811  0.03083497
#>  [7,]  1.000000000  1.000000000  1.000000000  1.00000000  1.00000000
#>  [8,]  0.219663372  0.218514458  0.238367849  0.11211551  0.16907227
#>  [9,]  0.515985171  0.515245614  0.238063342  0.14381810  0.15147992
#> [10,] -0.330324480 -0.326315240 -0.198545769 -0.25254440 -0.26249934
#> [11,]  0.480509687  0.452726283  0.449674348  0.41564975  0.18627580
#> [12,]  0.219663372  0.218514458  0.238367849  0.11211551  0.16907227
#> [13,]  1.000000000  1.000000000  1.000000000  1.00000000  1.00000000
#> [14,]  0.296917656  0.301291880  0.193232806  0.25305895  0.25559216
#> [15,] -0.054983098 -0.036957112 -0.002945164  0.06581515  0.02898498
#> [16,]  0.408377521  0.393041092  0.331180263  0.31402514  0.25898383
#> [17,]  0.515985171  0.515245614  0.238063342  0.14381810  0.15147992
#> [18,]  0.296917656  0.301291880  0.193232806  0.25305895  0.25559216
#> [19,]  1.000000000  1.000000000  1.000000000  1.00000000  1.00000000
#> [20,] -0.001257366  0.007479881 -0.166536844 -0.10738211 -0.11164193
#> [21,] -0.180874381 -0.199955662 -0.191972166 -0.19437788 -0.13941943
#> [22,] -0.330324480 -0.326315240 -0.198545769 -0.25254440 -0.26249934
#> [23,] -0.054983098 -0.036957112 -0.002945164  0.06581515  0.02898498
#> [24,] -0.001257366  0.007479881 -0.166536844 -0.10738211 -0.11164193
#> [25,]  1.000000000  1.000000000  1.000000000  1.00000000  1.00000000
#>             [,18]       [,19]        [,20]
#>  [1,]  1.00000000  1.00000000  1.000000000
#>  [2,]  0.04340762  0.05495704  0.008884942
#>  [3,]  0.15837422  0.18578819  0.189796935
#>  [4,]  0.27371257  0.29514250  0.275192864
#>  [5,] -0.10605329 -0.05860514 -0.120088774
#>  [6,]  0.04340762  0.05495704  0.008884942
#>  [7,]  1.00000000  1.00000000  1.000000000
#>  [8,]  0.14329506  0.16426209  0.155155860
#>  [9,]  0.16735319  0.19262976  0.195762287
#> [10,] -0.22679730 -0.18124775 -0.132114057
#> [11,]  0.15837422  0.18578819  0.189796935
#> [12,]  0.14329506  0.16426209  0.155155860
#> [13,]  1.00000000  1.00000000  1.000000000
#> [14,]  0.21300958  0.32571085  0.323781049
#> [15,] -0.01938507  0.07497370  0.062455982
#> [16,]  0.27371257  0.29514250  0.275192864
#> [17,]  0.16735319  0.19262976  0.195762287
#> [18,]  0.21300958  0.32571085  0.323781049
#> [19,]  1.00000000  1.00000000  1.000000000
#> [20,] -0.06507791  0.12930939  0.134049225
#> [21,] -0.10605329 -0.05860514 -0.120088774
#> [22,] -0.22679730 -0.18124775 -0.132114057
#> [23,] -0.01938507  0.07497370  0.062455982
#> [24,] -0.06507791  0.12930939  0.134049225
#> [25,]  1.00000000  1.00000000  1.000000000